Sudoku puzzles appear in newspapers, magazines and on the Internet. But do you know how to solve them? This first installment of The Daily Standard's sudoku guide will get you started with the basics.

A sudoku puzzle (pronounced as three syllables soo-DOH-koo, or soo-doh-koo) is similar to a crossword puzzle, but instead of filling in blank cells with letters to make words, numbers are filled in so that each row, column and 3x3 box contain the numbers one through nine. Because each row, column and 3x3 box contains nine cells, each of the numbers one through nine will be used exactly once in each row, column or box. Although most sudoku puzzles use numbers, any set of nine characters or symbols can be used.

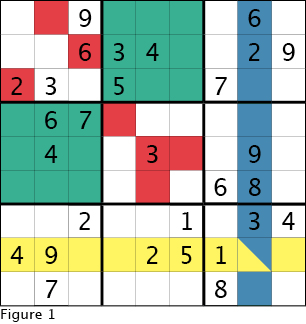
First, before we start working through an example puzzle, we should settle on some terminology for use in this guide. A cell is the basic unit of a sudoku puzzle. Cells are the smallest boxes in a puzzle. In one cell, you can fit one number, as illustrated by the seven small red squares in Figure 1. A row is a grouping of nine cells one cell high and nine cells wide shown by the nine yellow cells in Figure 1, and similarly a column is a set of cells one cell wide and nine cells high and illustrated by nine blue cells in Figure 1. A 3x3 box is a group of nine cells three cells wide and three cells high as shown by the two large teal squares in Figure 1. The nine 3x3 boxes in a sudoku puzzle are delineated by the bold lines.

The basic premise of solving a sudoku puzzle is to place the numbers one through nine exactly once in each row, column and 3x3 box based on the starting numbers that are already filled in and any subsequent numbers you fill in. This should be done by logic rather than guessing.

There are many different strategies and techniques people use to solve sudoku puzzles. There does seem to be two general schools of thought though. One involves making pencil marks in cells that denote which numbers can possibly be placed in that cell. When this technique works most elegantly, it leaves only one possibility in a cell. This approach is more suited to solving puzzles online where the interface can automatically fill in these numbers. Another school of thought is to reason out where a number must go in a particular row, column or 3x3 box. In this first lesson, we will stick to very basic techniques that will more closely follow the later style. But more difficult puzzles will require a combination of both styles.

In this lesson, we will use the easy sudoku puzzle in Figure 2. I will demonstrate several solving techniques so you get a feeling for how to fill in numbers. What I am explaining here are the highlights. Finding these highlights. is what takes most of the time, and makes filling in a number satisfying. As you are just starting out, the searching part will take some time, but do try to persevere and not become frustrated.

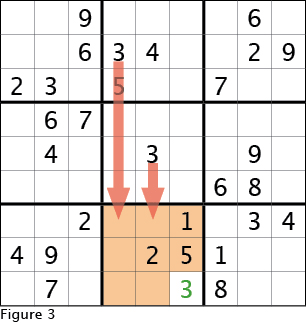
The very first technique we will use is some times called "hidden singles." Look at the bottom center 3x3 box in Figure 2. Notice that the three in this 3x3 box is not filled in. Now look at the two 3x3 boxes above this 3x3 box and see that the three is filled in each of them. Remember that the cardinal rule is that there must be exactly one of each number is every row, column and 3x3 box. This means that the bottom 3x3 box needs to have its three filled in, and that its three cannot be in the same columns as the threes in the two 3x3 boxes above. Looking at Figure 3, we see the left and center columns in the bottom 3x3 box cannot contain the required three and in the right column two of the three cells are already filled. So the three must go in the bottom right corner of this 3x3 box as seen in Figure 3.

Using this same logic, look at the 3x3 box in the bottom right of the puzzle. Notice that the nine is not filled in yet. Now look at the two 3x3 boxes above and see that the center and right columns of each of these boxes have nines in them. Looking back at the bottom 3x3 box we see that the nine can not be in the center or right columns, and two of the left columns are already filled. So, as this logic illustrates in Figure 4, the nine must be in the upper left cell of this 3x3 box.

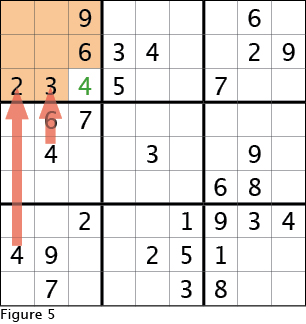
One more time, this time looking at the upper left 3x3 box, see that the four is not filled in. Now look at the two 3x3 boxes below this and see that each one has a four filled in; one is in the first column, and the other in the second column. Looking back at the top 3x3 box, the four must go in the one open cell in the third column, as show in Figure 5.

This same logic applies to filling in the two in the center left 3x3 box as seen in Figure 6. This time notice that the positions of twos in the 3x3 boxes above and below are taken into account.

Note that all of the above cells could have been done in any order. And although I have pointed out these instances of filling in cells very rapidly, I found them by slowly and methodically going through all the numbers in all of the 3x3 boxes.

So far we have only been looking vertically. If we look at the lower left 3x3 box, we see that we still need to fill in the three. Now, looking at the bottom right 3x3 boxes the three is in the top row. And looking at the bottom middle 3x3 box, we see the three in the bottom row, which we filled in when we started working this puzzle. A number we fill in is as valid to use as a clue as the starting, filled-in cells, unless of course a mistake was made. This means that the three in the lower left 3x3 box must be in the middle row, and furthermore in the only unfilled cell in the middle row. See Figure 6 to visually follow this.

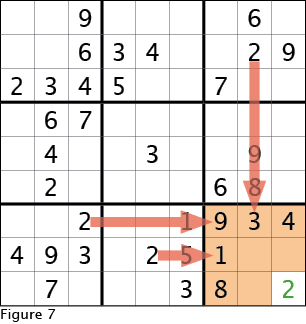
To this point we have just been looking in one direction when eliminating a potential cell. To take one step beyond this, look at the lower right cell again. In one of the four empty cells we will need to place a two. Following along in Figure 7, we see that the two 3x3 boxes to the left contain twos, and these eliminate the possibility of placing the two in our target box in the top two rows (well, the top row is already completely filled). This leaves two potential cells for the two in the bottom row. Next, look vertically and spot the two in the top right 3x3 box. This two eliminates the possibility of placing the two in one of the remaining cells in the lower 3x3 box, thus the two must be in the very lower right cell.

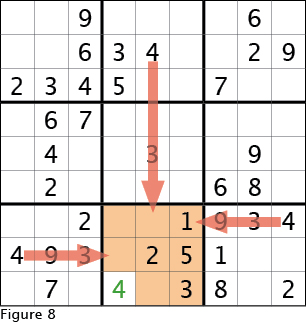
To illustrate looking in two directions again, see Figure 8 and the lower center 3x3 box. Here we will place the four. Looking to the right and to the left, the fours in those 3x3 boxes mean the four in the center box must be in the bottom row. The cell in the right column was the first we filled, which leaves two open cells in the bottom row. Looking up at the two 3x3 boxes above, sure enough, there is a four in the center column of the top box. Eliminating the center box in the bottom row leads to only one possibility for placing the four.

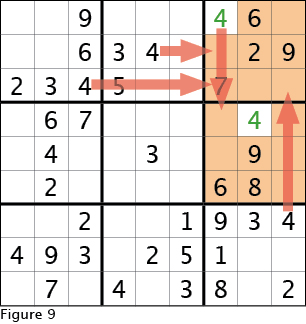
Sticking with the fours, look at Figure 9 to see how using clues in two directions can solve the problem for the four in the upper right 3x3 box. Then use this four to place the four in the 3x3 box directly below (this only requires looking in one direction).

Quickly, focusing on the lower right 3x3 box in Figure 10, note that there is only one possible location for the five and one possible location for the six.

Now that the lower right 3x3 box is filled in with all but one number, we can illustrate the second group of solving techniques in this lesson. If you have any trepidation, then fear not, these are even easier than what we covered previously.

OK, looking at the lower right 3x3 box, there is one empty cell and one missing number. Needing one of every number in each 3x3 box, row and column, this cell must be filled with seven.

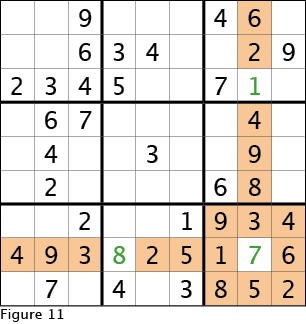
Now, looking at the row second from the bottom (see Figure 11) we see that it has only one empty cell, and one missing number, so we can fill the empty cell with eight to complete the row.

Staying with Figure 11, we can see that there is only one missing number and one empty cell in the column that is second from the right. Thus this empty cell must be filled in with one.

These last three illustrate how to fill in missing singles, in 3x3 boxes, rows and columns - the easiest way to fill in numbers.

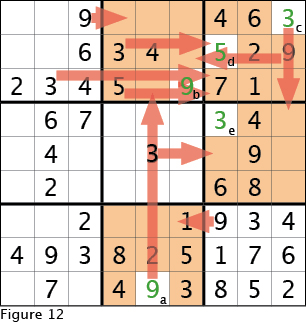
To illustrate this one more time, look at Figure 12 and see which new cells are filled in. Reassure yourself that you understand the logic that led to these cells being filled in based on the techniques we discussed above. Then refer to Figure 13 to see which cells can be filled in because they are the only empty cells in a row, column or 3x3 box. There is only one empty cell in the upper right 3x3 box, and thus one missing number. Filling this cell in with eight completed the 3x3 box. Filling in this cell makes the third row from the top complete with the exception of one cell. Marking this cell with the missing six will complete the row. And looking at the third column from the right, you can see that the one missing cell must be a two.

At this point, you know and understand all the basics you need to complete this sudoku puzzle and almost all other sudoku puzzles rated easy.

Use the completed solution in Figure 14 to check your progress as you finish this puzzle. As this is presumably your first puzzle, this may take you some time, but that will just make the completed solution more gratifying. I recommend taking a combination of these two strategies: Look for rows, columns and 3x3 boxes that have a few empty cells and see if you can fill in one or two. And be somewhat methodical to be sure you go through all rows, columns and 3x3 boxes and all numbers one through nine.