The first installment of The Daily Standard's sudoku guide demonstrated how to solve easy puzzles using two techniques. In this second edition, the previous techniques will be employed, but when their limitations are reached, a new approach will be introduced.

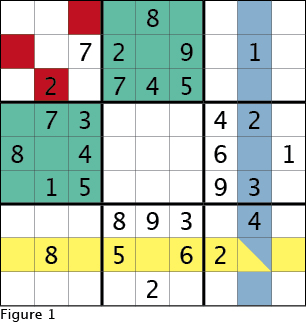
A sudoku grid consists of a square of 81 cells nine cells wide and nine cells high. Cells are the small red squares in Figure 1. One and only one number can be placed in each cell. Figure 1 also is the starting grid for this installment's example puzzle. A row is a grouping of nine cells, one cell high and nine cells wide. Conversely, a column is one cell wide and nine cells high. Note that in Figure 1 there are nine rows and nine columns even though only one row is highlighted in yellow and one column is marked in blue. Finally, a sudoku grid is divided into nine 3x3 boxes. The thick lines in Figure 1 delineate the 3x3 boxes and two 3x3 boxes are highlighted in green.

The cardinal rule for solving sudoku puzzles is to place the numbers one through nine exactly once in each row, column, and 3x3 box based on the numbers that are filled at the start and any numbers the player fills.

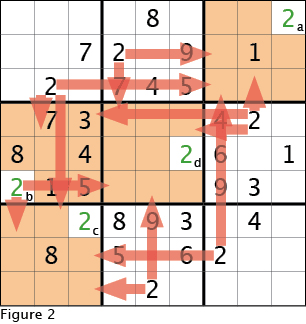
The first technique we learned in the previous edition was looking for "hidden singles" in the 3x3 boxes. Figure 2 shows how applying the cardinal rule can determine where the remaining twos must be placed. In the 3x3 boxes that don't already have a two, cells that are already filled are light orange to indicate a two can not be placed in them. And the orange arrows indicate that another two can not be in the light orange cells. As you inspect the logic for placing the twos in Figure 2, start with the cell labeled "a" and proceed in alphabetic order, as some of the later twos positions result from the locations of previous twos.

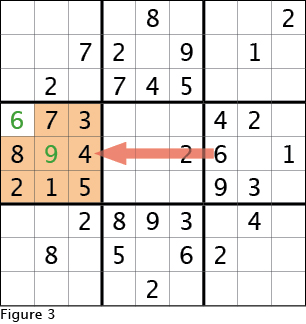
Another hidden single can be found in the left center 3x3 box. Figure 3 shows the six to the right leaves only one cell open to place the six in the left center 3x3 box. After the six is filled in, there is only one missing number from this 3x3 box and one empty cell, thus the nine goes in the center cell as illustrated by Figure 3. A situation such as this where there is one empty cell in a 3x3 box, row or column, is type of "naked single."

At this point, we have reviewed the content of the previous sudoku guide. While these techniques certainly are basic and applicable to every sudoku, they are not sufficient to solve sudoku puzzles with ratings other than "easy."

As was mentioned last time, there seem to be general schools of thought, or approaches, when it come to solving sudoku puzzles. One was covered previously and above where the player uses what is shown on the grid to decide which numbers go where. The second approach, which is more tedious, involves systematically putting marks into cells that indicate where a number can possibly be placed. When this works most elegantly, a cell will have only one possible number noted in it, and thus that number can be placed. Because marking all possibilities in cells, and updating possibilities every time a number is placed, can be tedious, sudoku puzzles done on a computer or on line will usually fill out the possibilities for you and update them automatically.

In this guide, I will mark possibilities in cells by writing a number in a certain location in each cell if that number could possibly be placed in that cell. Figure 4 shows the location each number will be noted in a cell if that number can be placed it that cell. The layout of numbers is that same as the key pad on a phone "dial."

You can mark possible locations of numbers in cells however you wish. You can note possible numbers along the top or bottom of the cell, willy-nilly anywhere in the cell you like, or as I demonstrated in grid pattern. If you use the grid pattern, you do not even have to use actual digits; you can put a dot in the location that would represent that number. This dot notation is especially useful if you tend to write large, or you have a small sudoku grid. All the methods mentioned so far require you to erase the number or dot when you discover that number is no longer a possibility for the cell.

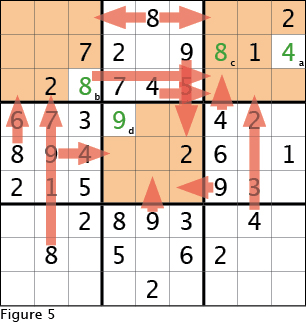
To solve our example puzzle, refer to Figure 5 and see we are still using methods learned last time to fill in four cells. Again, look at the logic behind each cell in alphabetical order as cell b is used to fill in cell c.

Look at Figure 6 where all possible values for each cell have been noted on a grid within each cell. Be sure you understand how these numbers are possibilities in the cells based on the filled-in numbers in a cell's row, column, and 3x3 box.

Looking at Figure 6, hopefully you spotted three cells that have only one possible number in them. These are the gems that you are hoping to find as you fill in possibilities. We can now see why these cells are called "naked singles" because they are not obfuscated by other possibilities in a cell.

Normally when solving a sudoku puzzle, you would fill all three of these cells with the only possible number, then eliminate possibilities in rows, columns and 3x3 boxes and finally fill in any naked singles that might result. But for this guide, I am going to proceed in a slightly different order.

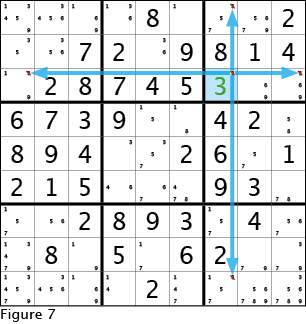
I am going to ignore the naked single one in the top center 3x3 box for now and look at the naked single three in the top right 3x3 box. Be sure to understand why three and only three can be placed in this cell. There is at least one instance of every number besides three in the top right 3x3 box, the third row from the top and the third row from the left. Follow along in Figure 7 as I show that once I fill the three in, I then must cross out the possibility of placing a three in the same 3x3 box, row and column. It is definitely the best practice to cross out these possibilities as soon as you fill in a number. Crossing out the possibilities when you get one big string of numbers to fill in can be hectic, but do try your best. It is in crossing out possibilities where computer assisted solving can really shine.

Filling this three and crossing out the possibilities has not led us to being able to fill in other cells, so we will proceed to the naked single three in the center 3x3 box. Figure 8 shows how placing this three affects the possibilities noted in the same column and row. Notice further that by eliminating the possibility of a three in the first column in the top center 3x3 box, there is only one possible location in that 3x3 for the three to be placed. This is not illustrated in Figure 8 but you can see that once the three is placed in the very center of the top center 3x3 box, there remains only one location in this 3x3 box where the six could be placed. After placing these two numbers, and crossing out the possible threes and sixes in corresponding rows and columns in other 3x3 boxes, you can see that a cascade of other cells can be filled in and those lead to other cells' solutions. In fact if we followed this cascade (or the cascade that would result from filling in the one in the top center 3x3 box) we are able to solve the entire sudoku puzzle. But if we did that we wouldn't learn about hidden singles.

Hidden singles are the only possibility for a particular number in a particular row, column or 3x3 box. They are termed "hidden," as opposed to "naked," because their locations are obscured by the presence of other possibilities. Figure 9 shows the locations of hidden singles in this lesson's example sudoku. Cell a is the only possible location for a one in the third row from the top. Cell b is the only possible location for a four in the second row from the bottom. Cell c is the only possible location for an eight in the second column from the right. And cell d is the only possible location for a three in the center column and the top center 3x3 box. Using the techniques we learned last time, we have already rooted out all other hidden singles in the 3x3 boxes. You now understand why I called them hidden.

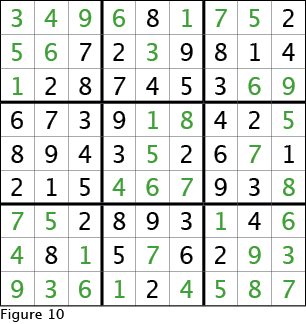
In Figure 9, you can fill in all of the hidden and naked singles in the grid and by using all techniques we have discussed in this session and last, you are now equipped with the knowledge you need to solve most sudoku puzzles labeled easy and moderate. Be sure to do your best to eliminate possibilities in other cells as you fill in numbers. Figure 10 shows the completed solution.